الإنحدار الخطي باستخدام برنامج بايثون Python

الأنحدار الخطي (linear regression) هو أسلوب إحصائي يهدف لإيجاد علاقة خطية بين المتغير التابع (dependent variable) والمتغيرات المستقلة (independent variables)، كذلك يهدف الى التنبؤ (prediction) بقيم المتغير التابع. ويمكن تعريف الإنحدار الخطي رياضياً كما يلي:

\[
y=\alpha+\beta_1 x_1+\beta_2 x_2+…+\beta_p x_p+\epsilon
\]

حيث يسمى $y$ المتغير التابع (dependent variable) او متغير الإستجابة (response variable) او متغير الناتج (outcome variable)، كذلك تسمى $x_1, x_2,…, x_p$ المتغيرات المستقلة (independent variables) او المتغيرات التفسيرية (explanatory variables) او متغيرات التنبؤ (predictor variables).

تُعرف البواقي (Residuals) بأنها الفرق بين القيمة الملاحظة (الفعلية) للمتغير التابع وقيمة المتغير التابع التي يتم التنبؤ بها بإستخدام خط الانحدار.

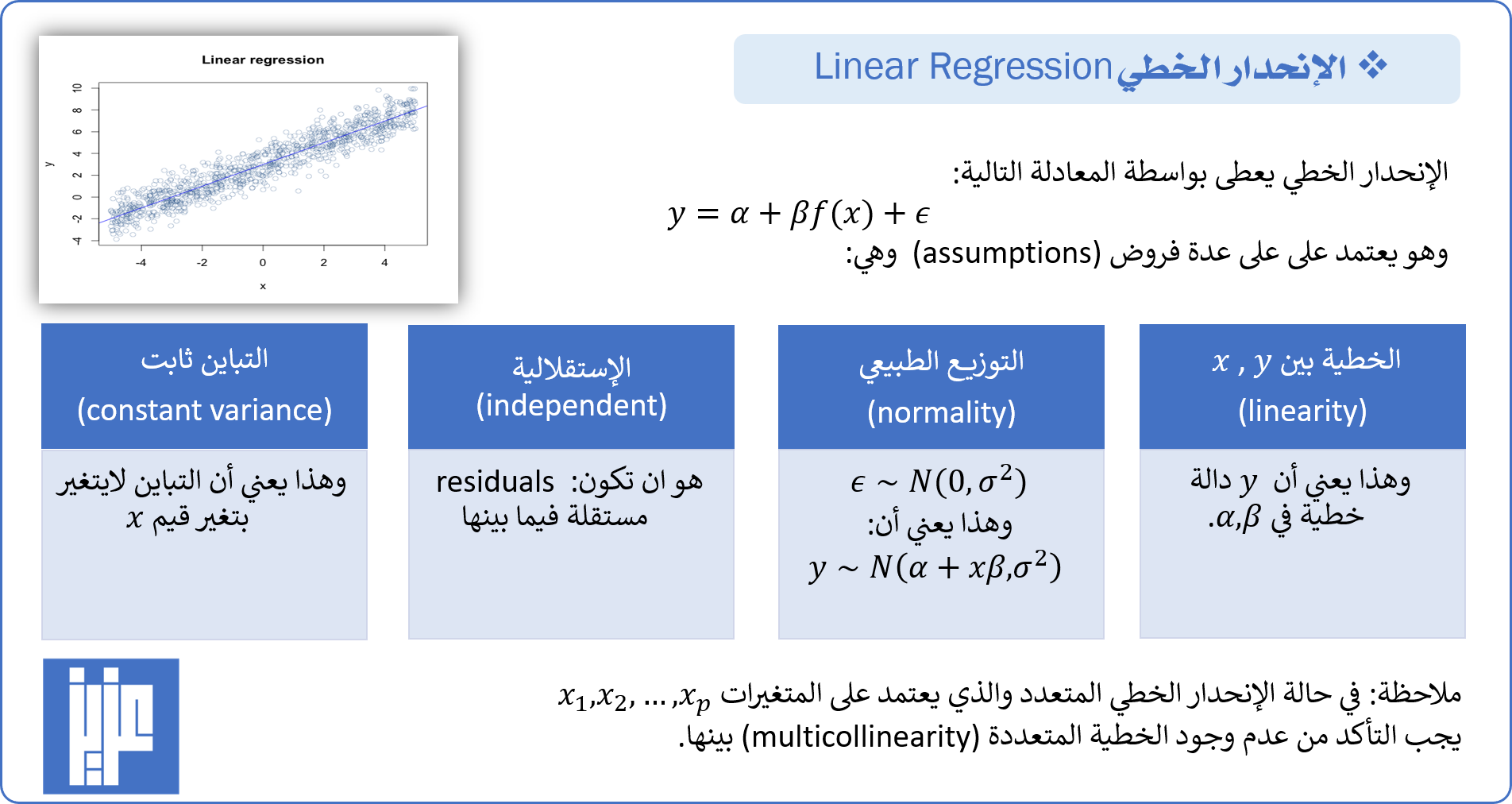
تعطى فروض الإنحدار الخطي (assumptions of linear regression) كما في الشكل ادناه:

الآن سوف نتناول تطبيق الإنحدار الخطي (Linear regression) في برنامج بايثون (Python). نقوم بتحميل بعض الحزم (packages) التي نحتاجها وهي:

In:
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn import datasets
import statsmodels.formula.api as smf
from statsmodels.graphics.gofplots import ProbPlot

كذلك نقوم بتحميل البيانات التي سوف نستخدمها وهي diabetes dataset  تحوي 442 مشاهدة و 10 متغيرات وهي العمر ، الجنس ، مؤشر كتلة الجسم ، متوسط ضغط الدم ، وستة قياسات لمصلية الدم  وهي متوفرة من خلال حزمة sklearn:

In:
diabetes = datasets.load_diabetes()
x = np.concatenate(diabetes.data[:, np.newaxis, 2])
y = diabetes.target
mydata = pd.DataFrame({'x':x, 'y':y})

نلاحظ أن تم إختيار متغيرين تمت تسميتها x و y وتم تخزينا في بيانات جديدة mydata لإستخدامها في شرح هذا الموضوع، مع ملاحظة أنه يمكن استخدام جميع البيانات. اولاً: نرسم شكل الإنتشار والذي يمثل العلاقة بين المتغيرين باستخدام الكود:

In:
plt.scatter(x, y)
plt.xlabel("x")
plt.ylabel("y")
plt.show()

والذي يعطي الشكل التالي:

ثم نقوم بنمذجة هذه العلاقة باستخدام الإنحدار الخطي كما يلي:

In:
model_f='y~x'
model = smf.ols(formula=model_f, data=mydata)
model_fit = model.fit()

حيث يمكن تصوير هذا النموذج الخطي باستخدام الكود:

In:
fitted_values=model_fit.fittedvalues
plt.scatter(x, y)
plt.plot(x, fitted_values, c='r')
plt.xlabel("x")
plt.ylabel("y")
plt.show()

والذي يعطي النتيجة التالية:

كما يمكن عرض ملخص نتائج هذا النموذج باستخدام الدالة:

In:
print (model_fit.summary())
Out:
                            OLS Regression Results                            
==============================================================================
Dep. Variable:                      y   R-squared:                       0.344
Model:                            OLS   Adj. R-squared:                  0.342
Method:                 Least Squares   F-statistic:                     230.7
Date:                Sat, 27 Oct 2018   Prob (F-statistic):           3.47e-42
Time:                        11:39:03   Log-Likelihood:                -2454.0
No. Observations:                 442   AIC:                             4912.
Df Residuals:                     440   BIC:                             4920.
Df Model:                           1                                         
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
Intercept    152.1335      2.974     51.162      0.000     146.289     157.978
x            949.4353     62.515     15.187      0.000     826.570    1072.301
==============================================================================
Omnibus:                       11.674   Durbin-Watson:                   1.848
Prob(Omnibus):                  0.003   Jarque-Bera (JB):                7.310
Skew:                           0.156   Prob(JB):                       0.0259
Kurtosis:                       2.453   Cond. No.                         21.0
==============================================================================

كذلك يمكن الحصول على الاشكال اللازمة للتأكد من فروض النموذج الخطي (Diagnostic Plots) وأهمها:

اولاً: QQ-plot والذي يستخدم للتأكد من أن البواقي (residuals) تتبع التوزيع الطبيعي (Normal distribution). والذي يمكن الحصول عليه باستخدام الكود:

In:
residuals = model_fit.resid
studentized_residuals = model_fit.get_influence().resid_studentized_internal

QQ = ProbPlot(studentized_residuals)
plot=QQ.qqplot(line='45', alpha=0.5, color='#4C72B0', lw=1,ylabel='Standardized Residuals')


plt.title('Normal Q-Q')
plt.xlabel('Theoretical Quantiles')
plt.ylabel('Standardized Residuals')

top_abs_studentized_residuals = np.flip(np.argsort(np.abs(studentized_residuals)), 0)[:3]
for r, i in enumerate(top_abs_studentized_residuals):
    plt.annotate(i, xy=(np.flip(QQ.theoretical_quantiles, 0)[r],studentized_residuals[i]))

والذي يعطي الشكل:

ثانياً: Residuals vs Fitted values وهو مفيد للتأكد من فرض الخطية وتجانس التباين ( the assumption of linearity and homoscedasticity)، حيث يأخذ شكل إنتشار عشوائي حول الصفر والذي يمثل تقريباً منتصف المحور العامودي الذي يمثل البواقي الموجبة والسالبة. كذلك يجب أن لايكون هناك اي مشاهدة خارج الإنشار بشكل واضح (شاذة او متطرفة). والذي يمكن الحصول عليه باستخدام الكود:

In:
plot = sns.residplot(fitted_values, 'y', data=mydata, 
                          lowess=True, 
                          scatter_kws={'alpha': 0.5}, 
                          line_kws={'color': 'red', 'lw': 1, 'alpha': 0.8})

plt.title('Residuals vs Fitted values')
plt.xlabel('Fitted values')
plt.ylabel('Residuals')

abs_residuals=np.abs(residuals)
top_abs_residuals = abs_residuals.sort_values(ascending=False)[:3]

for i in top_abs_residuals.index:
    plt.annotate(i, xy=(fitted_values[i], residuals[i]))

والذي يعطي الشكل:

ثالثاً: Scale-Location وهو مفيد للتأكد من فرض تجانس التباين ( the assumption of homoscedasticity)، حيث يأخذ شكل إنتشار عشوائي ولا يأخد شكل منتظم متزايد او متناقص. والذي يمكن الحصول عليه باستخدام الكود:

In:
abs_sqrt_studentized_residuals = np.sqrt(np.abs(studentized_residuals))
plt.scatter(fitted_values, abs_sqrt_studentized_residuals, alpha=0.5)
sns.regplot(fitted_values, abs_sqrt_studentized_residuals, 
            scatter=False, 
            ci=False, 
            lowess=True,
            line_kws={'color': 'red', 'lw': 1, 'alpha': 0.8})

plt.title('Scale-Location')
plt.xlabel('Fitted values')
plt.ylabel('$\sqrt{|StandardizedResiduals|}$')


 
top_abs_sqrt_studentized_residuals= np.flip(np.argsort(abs_sqrt_studentized_residuals), 0)[:3]
for i in top_abs_sqrt_studentized_residuals:
    plt.annotate(i, xy=(fitted_values[i], abs_sqrt_studentized_residuals[i]))

والذي يعطي الشكل التالي:

رابعاً: Residuals vs Leverage والذي يستخدم لقياس تأثير كل مشاهدة على معاملات (coefficients) الانحدار الإنحدار الخطي. والذي يمكن الحصول عليه باستخدام الكود:

In:
model_leverage = model_fit.get_influence().hat_matrix_diag
cooks_distance = model_fit.get_influence().cooks_distance[0]
plt.scatter(model_leverage, studentized_residuals, alpha=0.5)
sns.regplot(model_leverage, studentized_residuals, 
            scatter=False, 
            ci=False, 
            lowess=True,
            line_kws={'color': 'red', 'lw': 1, 'alpha': 0.8})

plt.xlim(0,0.035)
plt.title('Residuals vs Leverage')
plt.xlabel('Leverage')
plt.ylabel('Standardized Residuals')

top_leverage= np.flip(np.argsort(cooks_distance), 0)[:3]
for i in top_leverage:
    plt.annotate(i, xy=(model_leverage[i],studentized_residuals[i]))

والذي يعطي الشكل:

كما يمكن إضافة حدود Cook’s distance بإضافة الاسطر التالية للكود السابق:

In:
plt.ylim(-3,8)
r = np.linspace(0.001, 0.035, 50)
p = len(model_fit.params)
d = np.sqrt((0.5 * p * (1 - r)) / r)
plt.plot(r, d, label='Cook\'s distance', lw=1, ls='--', color='red')
plt.legend(loc='upper right')

ليعطي الشكل التالي: