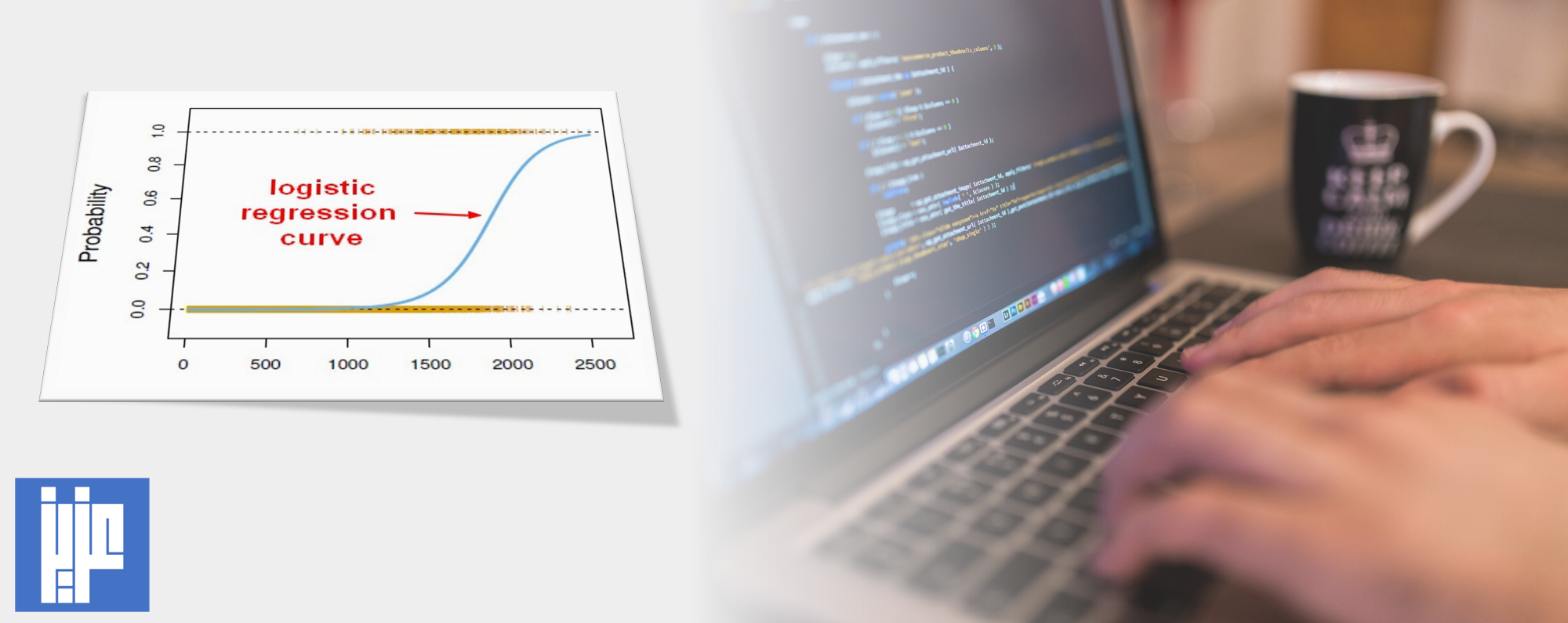
الانحدار اللوجستي (logistic regression) باستخدام بايثون Python

الانحدار اللوجستي (logistic regression) هو أسلوب إحصائي يستخدم لوصف العلاقة بين متغير تابع (dependent variable) ثنائي (binary) ومتغير مستقل (independent variable) واحد او أكثر وفق الصيغة التالية:

\[
logit(p)=\alpha+\beta X
\]

حيث

\[
logit(p)=\ln{\left(\frac{p}{1-p}\right)}
\]

وكذلك $$p=p(y=1|X)$$.

ملاحظة: في تعلم الآلة، يعرف المتغير التابع (dependent variable) بالمتغير الهدف (target variable). كذلك تعرف المتغيرات المستقلة (independent variables) بمتغيرات التنبؤ (predictor variables) او الخصائص (features).

وهناك عدد من الفروض (assumptions) الهامة التي ينبغي التنبه لها عند استخدام الانحدار اللوجستي وهي:

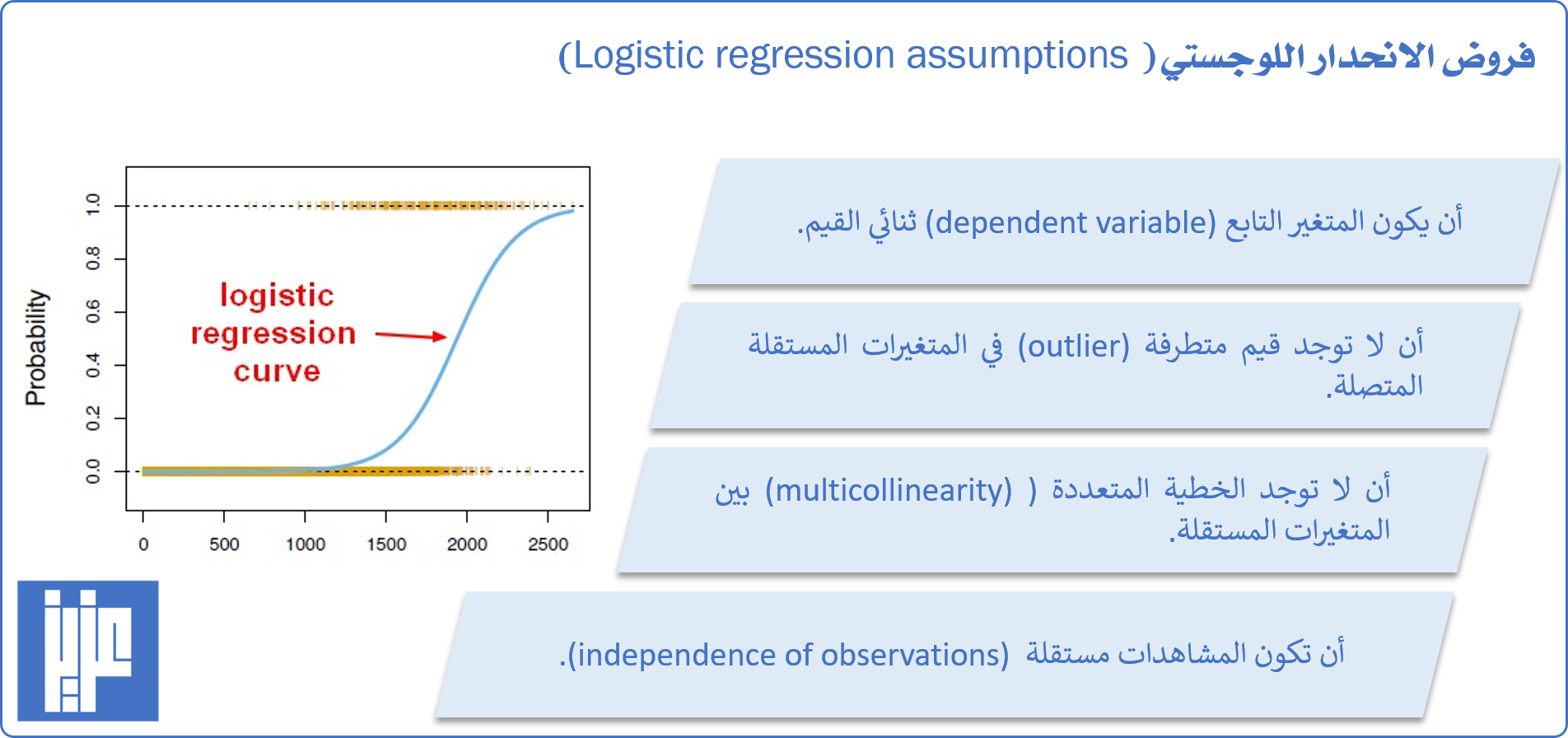
الآن سوف نوضح كيف يمكن تطبيق نموذج الانحدار اللوجستي على البيانات: Breast Cancer Wisconsin Data Set وذلك باستخدام لغة البرمجة بايثون. المزيد من التفاصيل حول هذه البيانات على الرابط. للقيام بذلك سوف نتبع الخطوات التالية:

1. تحميل البيانات:

In:
import pandas as pd 
wdbc_data = pd.read_csv('wdbc.csv',sep=',')
wdbc_data.head()
Out:
         id diagnosis  radius_mean  ...  concave points_worst  symmetry_worst  fractal_dimension_worst
0    842302         M        17.99  ...                0.2654          0.4601                  0.11890
1    842517         M        20.57  ...                0.1860          0.2750                  0.08902
2  84300903         M        19.69  ...                0.2430          0.3613                  0.08758
3  84348301         M        11.42  ...                0.2575          0.6638                  0.17300
4  84358402         M        20.29  ...                0.1625          0.2364                  0.07678

في هذه الحالة سوف يكون المتغير التابع (المتغير الهدف) هو diagnosis وهو ثنائي كما يتضح من التالي:

In:
wdbc_data['diagnosis'].value_counts()
Out:
B    357
M    212
Name: diagnosis, dtype: int64

حيث يمثل هذا المتغير تشخيص الخلايا السرطانية الى خبيثة (M) او حميدة (B)، وجميع المتغيرات المتبقية هي متغيرات مستقلة (خصائص). سوف يتم تخزين المتغير التابع diagnosis في المتغير y بعد استبدال M بـ 1 و B بـ 0، كذلك سوف يتم تخزين المتغيرات المستقلة في المصفوفة X كما يلي:

In:
wdbc_data['diagnosis']=wdbc_data['diagnosis'].replace('M',1 )
wdbc_data['diagnosis']=wdbc_data['diagnosis'].replace('B', 0)
y = wdbc_data['diagnosis']
X = wdbc_data.iloc[0:, 2:32]

2. تقسيم البيانات الى مجموعة تدريب (train) ومجموعة اختبار (test):

سوف نقوم في هذه الخطوة بتقسيم البيانات الى مجموعتين واحدة لتدريب النموذج والاخرى لاختباره لاحقاً، وذلك باستخدام الكود:

In:
from sklearn.model_selection import train_test_split
y_train,y_test,X_train,X_test = train_test_split(y,X,test_size = .2) 

3. تطبيق نموذج الانحدار اللوجستي:

في هذه الخطوة سوف نقوم بتطبيق النموذج على مجموعة التدريب من خلال الدوال التالية:

In:
from sklearn.linear_model import LogisticRegression
logist_model=LogisticRegression()
logist_model.fit(X_train,y_train)

يمكن الحصول على على قيم المعاملات (coefficients) بإستخدام الدالة:

In:
logist_model.coef_

حيث يجب تحديد المتغيرات المستقلة الهامة التي يجب ان تكون في النموذج واستبعاد الأخرى للوصول لأفضل نموذج يجب تطبيقه، كذلك من المهم التأكد من تحقق الفروض الخاصة بالانحدار اللوجستي، وكذلك التأكد من عدم وجود خطية متعددة (multicollinearity) او قيم متطرفة (outliers).

 4. التحقق من صحة النتائج (validation):

في هذه الخطوة سوف نقوم باستخدام مجموعة الاختبار للتحقق من دقة النموذج المستخدم وذلك من خلال:

• مصفوفة الخطأ (confiusion matrix):

حيث يمكن استخدام الكود:

In:
from sklearn import metrics
from mlxtend.plotting import plot_confusion_matrix
y_pred=logist_model.predict(X_test)
cm = metrics.confusion_matrix(y_test, y_pred)
plot_confusion_matrix(cm)

والذي يعطي النتيجة التالية:

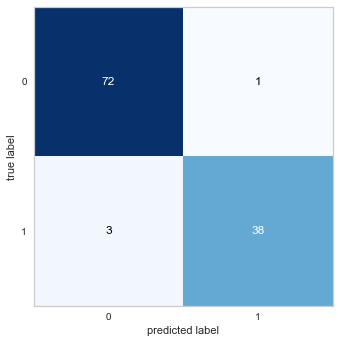
• معدل الدقة (Accuracy) والإحكام (Precision) :

وذلك من خلال استخدام الدوال التالية:

In:
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))
print("Precision:",metrics.precision_score(y_test, y_pred))
Out:
Accuracy: 0.96
Precision: 0.97